課本: Introduction to Information Retrieval

CH8 Evaluation in information retrival

評量 search engine 好壞

1. 搜到的 index
2. 搜尋速度
3. 二氧化碳排放量
4. 和搜尋相關程度

相關程度

1. benchmark 資料集
2. benchmark queries(問句)
3. 文章是否相關的標記(ground truths)

queries 和 information need 有落差 想找的東西,不會下 key word

Precision (P)

Precision = $\frac{檢索到相關物件的數量}{物件總數}$

Recall (R)

Recall = $\frac{檢索到相關物件的數量}{相關物件總數}$

true positive(tp) 機器判斷+且為真
false positive(fp)機器判斷+但是是假
false negatives(fn) 機器判斷-但判斷錯
true negatives(tn) 機器判斷-且判斷對

P = $\frac{tp}{tp+fp}$

R = $\frac{tp}{tp+fn}$

Accuracy vs Precision
accuracy = $\frac{tp+tn}{tp+fp+fn+tn}$

accuracy 不適合用在 information retrieval, 因為通常 Nonrelevant 會非常的大,tn 項非常大除分母 fn 和 tn 都非常大結果會趨近於 1,所以才用 Precision 和 Recall 作為依據

調和平均數(harmonic mean)

H = $\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+..+\frac{1}{x_n}}$

Precision/Recall Tradoff 使用調和平均數計算 Precision 和 Recall 的 Tradoff
量測的數值稱做 F measure,α和 1-α分別為 P 和 R 的權重,一般是取α=0.5
(P 和 R 重要程度相同)

F = $\frac{1}{\alpha\frac{1}{P}+(1-\alpha)\frac{1}{R}} = \frac{(\beta^2+1)PR}{\beta^2P+R}$ where $\ \beta^2=\frac{1-\alpha}{\alpha}$

Ranked Evalution

P,R,F 都是 unordered(沒有等級)
一個 query 會有一個 Precision/Recall 圖
使用內插法(interpolated)可以得到一張較平滑的 P-R 圖
(和機器學習 ROC curve 相似)
P-R curve 的面積越大效能越佳(代表 Precision 掉越慢)

內插法

$\ p_{interp}= \max\limits_{r'\ge r}\ p(r{'})$

r 代表 recall, 作法是從目前往後找最高的點向前填平,並重新畫 P-R 圖

Mean Average Precision(MAP)

$\ MAP(Q) = \frac{1}{|Q|}\sum^{|Q|}_{j=1}\frac{1}{m_j}\sum_{k=1}^{m_j}Precision(R_{jk})$

第一個 sum 算 query 平均
第二個 sum 算 precision 平均

Precision at k
第 k 個搜索結果的 Precision

R-Precision
文件中總共有 R 篇相關文章,以 R 作為 cut-off,計算 Precision
e.g. 總共有 100 篇文章,其中 10 篇是相關的
且搜尋結果是:RNRNN RRNNN RNNRR …
R=10(只看 RNRNN RRNNN)計算 Precision
R-Precision = 0.4

Normalized Discounted Cumulative Gain(NDCG)
作者：Kalervo Jarvelin, Jaana Kekalainen(2002)

用來衡量 ranking quality

e.g.
G = <3,2,3,0,0,1,2,2,3,0,…>
G 表示一個搜索的結果(3 高度相關, 0 沒關係)
步驟:

1. Cumulative Gain(CG)

   $$CG[i] = \left\{\begin{matrix} G[1], &if\ i=1 \\ CG[i-1]+G[i], &otherwise \end{matrix}\right.$$

   目前項+＝前一項(做成一個遞增的函數) CG’=<3,5,8,8,8,9,11,13,16,16,…>

2. Discounted Cumulative Gain(DCG)

   $$DCG[i]=\left\{\begin{matrix} G[i], & if\ i=1\\ DCG[i-1]+G[i]/log_b\ i, & otherwise \end{matrix}\right.$$
   DCG’=<3,5,6.89,6.89,6.89,7.28,7.99,8.66,9.61,9.61,…> if b=2 i 代表排名,對排名做懲罰(除 log₂ i),排名越後面懲罰越重 代表如果搜尋的結果很差,和理想的排序分數會相差很多
3. Normalized Discounted Cumulative Gain(NDCG)
   理想的搜索結果 I=<3,3,3,2,2,2,1,1,1,1,0,0,0,…>(高度相關的排越前面)
   理想搜索結果 DCGI=<3,6,7.89,8.89,9.75,10.52,10.88,11.21,…>
   nDCG_n = $\ \frac{DCG_{n}}{IDCG_{n}}(\frac{相關程度排序}{理想相關程度},做正規化)$
   NDCG=<1,0.83,0.87,0.77,0.70,0.69,0.73,0.77,…>

benchmark 資料集

1. Cranfield
2. TREC(nist.gov)
   Ad-hoc 資料集(1992-1999)
3. GOV2 2500 萬篇文章
4. NICIR cross-language IR
5. Cross Language Evaluation
6. REUTERS

標記資料準則
Kappa measure

標記資料是否一致的衡量標準,若標記不一致資料中就沒有 truth

Kappa 計算公式

$\ \kappa = \frac{P(A)-P(E)}{1-P(E)}$

搜尋結果的呈現 Result Summaries

• 搜尋結果呈現：10 blue link
• 搜尋結果下方文字說明分為 Static 和 Dynamic Static:固定抽前 50 個字 Dynamic:利用 nlp 技術,根據搜索關鍵字動態做變化
• quicklinks
  底下多的連結

CH6 Model

• Vector Space Model
• Probabilistic Information Retrieval

|Empirical IR | Model-based IR| |暴力法|有理論模型| |heuristic|數學假設| |難推廣到其他問題|容易推廣到其他問題|

IR model 歷史

• 1960
  第一個機率模型
• 1970
  vector space model(75)
  classic probabilistic model(76)
• 1980
  non-class logic model(86)
• 1990
  TREC benchmark
  BM25/Okapi(94)
  google 成立(96)
  Language model(98)
• 2000
  Axiomatic model(04)
  Markov Random Field(05)
  Learning to rank(05)

Vector space

|Vocabulary|V = { $w_1,w_2,w_3,...w_v$ }| |Query|q =$\{q_1,q_2,...,q_m\}$| |Document 文章|${d_i} = \{ w_1,w_2,... \}$|
|Collection 文章集合|C = { $d_1,d_2,d_3,...$ }|
|R(q) query 的集合|R(q) ⊂ C|

目標是找到近似 query 的集合
策略:

1. Document select
   挑文件如果是相關就收到集合
   absolute relevance(系統必須決定是相關還是不相關)
2. Document ranking
   query 的結果>threshold 就收進去
   relative relevance(不必是 1 或 0,相近到一定程度就收進集合)

Probability Ranking Principle(PRP)

Robertson (1977)
相似度量測函數 f 滿足,

f()值越大表示有越大的機率越相似

Relevance 流派

• Similarity 相似度
  Vector space model(Salton et al,75)
• Probability of relevance 機率模型 Classical probaility Model(Robertson&Sparck Jones,76)
  Learning to Rank(Joachims,02, Berges et al,05)
• Probability inference 機率推論

Vector Space Model(VSM)
將 query 和 document 表示成向量形式(similar representation)
假設 Relevance(d,q) = similar(d,q)
利用 cosine 算相似度(1 ~ -1)
high dimension(index 的維度通常在 10 萬左右)
good dimension -> orthogonal
(好的維度切割應該是維度間彼此獨立(orthogonal),
但是通常很困難,例如 nccu 後面接 university 的機率很高)
VSM 優點: Empirically effective,直觀, 實作容易

VectorSpace 範例程式
Building a Vector Space Search Engine in Python

大致步驟

• 將所有文章使用 join()成為一個 string 包含所有文章內容
• 做 string clean 去除. , 多餘空白,並轉為小寫

• 將 clean 好的 string 利用空白切分成 words array,丟到Porter stem(去除字尾)

  Porter Stemming Algorithm 作者:Martin Porter(2006)

• 刪除重複的 word,使用 set 讓出現的 word 唯一
• 得到所有整理完的 words,做成 index(將每個 word 編號),類似字典的概念
• 將每篇文章分別建立自己的 vector,並統計每個 word 出現的次數(term frequecy)
• 將輸入的 query 做成 vector
• 利用兩個向量做 cosine 計算相關程度

相似度計算

1. Cosine Similarity

   cosine = $\frac{V_1 \cdot V_2}{\|V_1\|\|V_2\|}$

2. Jaccard Similarity

   相似度 = $\frac{交集}{聯集}$

TF-IDF Weighting

• TF(Term Frequency)
  word count,單純統計字數出現頻率
• IDF(Inverse Document Frequency)(反向的 TF)
  字的獨特性,如果某些字在很多篇文章出現次數都很高(例如:the,a,to,…)
  IDF 值就會很低(沒有鑑別度)
  IDF(t) = 1 + log(n/k) (n:篇數,k:字出現次數)
  例如文章總數是 1000(n=1000),所有文章都有出現 cat(k=1000),
  IDF = 1 + log(1000/1000) = 1
  如果只有 1 篇文章有出現 cat,
  IDF = 1 + log(1000/1) = 4

TF-IDF 計算方法:

weight(t,d) = TF(t,d) * IDF(t)

TF-IDF 範例程式
Tutorial: Finding Important Words in Text Using TF-IDF

Ch11 Probabilistic Information Retrieval

Probability theory

• Joint probability
  $P(A\cap B)$
• Conditional probability
  $P(A | B)$
  probability of A given that event B occurred.
• Chain rule
  $P(A,B) = P(A\cap B) = P(A|B)P(B) = P(B|A)P(A)$
• Partition rule
  $P(B) = P(A,B) + P(\bar{A},B)$

Chain rule example wiki

有兩個甕第一個甕放 1 個黑球 2 個白球,第二個甕放 1 個黑球 3 個白球
事件 A 是選到第一個甕,事件 B 是選到白球
$P(B|A)= \frac{2}{3}$ 在選到第一個甕的情況下拿到白球
$P(A,B)=P(B|A)P(A)=\frac{2}{3} \times \frac{1}{2}$

Bayes’ Rule
$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$

from chain rule: $P(A|B)P(B) = P(B|A)P(A)$

P(A)    : 事前機率(prior probability)
P(A|B)  : 事後機率(postior probability)
P(B|A)  : likelihood

The term likelihood is just a synonym of probability.

Odds
$O(A) = \frac{P(A)}{P(\bar{A})} = \frac{P(A)}{1-P(A)}$

an event provide a kind of multiplier for how probabilities change.

Probability of Relevance

• Random variables:

  • query Q
  • document D
  • relevance R ∈ {0,1}
    (1:相關,0:不相關)
• Goal: P(R=1|Q,D) to rank relevant
  利用 query 和 document 相似度的機率做排名

Refining P(R=1|Q,D) Methods

1. Conditional Models(Discriminative Models)

   • 利用各種方法找出機率 P = f(x)
   • 利用資料訓練參數
   • 利用 model 去排列未知的 document
     e.g. Learning to rank,類神經網路,…

2. Generative Models

   • compute the odd of O(R=1|Q,D) using Bayes’ rules
     先找出資料的分佈再做預測
   • How to define P(Q,D|R)
   • Document generation: P(Q,D|R)=P(D|Q,R)P(Q|R)
     query 放到條件 (e.g RSJ model)
   • Query generation: P(Q,D|R)=P(Q|D,R)P(D|R)
     document 放到條件 (e.g language model)

RSJ Model (Binary Independence Model)

利用Odd值做 ranking 的依據:
$O(R|D,Q) = \frac{P(R=1|D,Q)}{P(R=0|D,Q)} = \frac{ \frac{P(D|Q,R=1)P(R=1|Q)}{P(D|Q)} }{ \frac{P(D|Q,R=0)P(R=0|Q)}{P(D|Q)} } = \frac{P(D|Q,R=1)P(R=1|Q)}{P(D|Q,R=0)P(R=0|Q)} \quad(1)$

$\frac{P(R=1|Q)}{P(R=0|Q)}$ 對 document ranking 沒有影響,視為常數

$\frac{P(D|Q,R=1)}{P(D|Q,R=0)} = \prod_{t=1}^{M} \frac{P(D_t|Q,R=1)}{P(D_t|Q,R=0)} \quad(2)$

將 document 拆成多個獨立的 document term 連乘積,且$D_t \in \{0,1\}$

$O(R|D,Q) = O(R|Q) \cdot \prod_{t=1}^{M} \frac{P(D_t|R=1,Q)}{P(D_t|R=0,Q)} \quad(3)$

(2)代入(1)可以整理出(3)

$O(R|D,Q) = O(R|Q) \cdot \prod_{t:D_t=1}^{M} \frac{P(D_t = 1|Q,R=1)}{P(D_t = 1|Q,R=0)} \cdot \prod_{t:D_t=0}^{M} \frac{P(D_t = 0|Q,R=1)}{P(D_t = 0|Q,R=0)}\quad(4)$

將 document term 分為出現或是不出現,(3)→(4)

$p_t = P(D_t = 1|Q,R=1)$

$u_t = P(D_t = 1|Q,R=0)$

$p_t$ 表示 term 出現在 document 且和 query 相關的機率
$u_t$ 表示 term 出現在 doucment 且和 query 不相關的機率

$O(R|D,Q) = O(R|Q) \cdot \prod_{t:D_t=Q_t=1} \frac{p_t}{u_t} \cdot \prod_{t:D_t=0,Q_t=1} \frac{1-p_t}{1-u_t} \quad(5)$

假設$Q_t = 0 \; then \; p_t = u_t$(假設可以做改變)
意思是沒出現在 query 的 term 就不用考慮,只考慮$Q_t = 1$
左邊連乘積表示 query term found in document
右邊連乘積表示 query term not found in document

$O(R|D,Q) = O(R|Q) \cdot \prod_{t:D_t=Q_t=1} \frac{p_t(1-u_t)}{u_t(1-p_t)} \cdot \prod_{t:D_t=0,Q_t=1} \frac{1-p_t}{1-u_t} \cdot \frac{1-p_t}{1-u_t} \quad(6)$

右邊連乘積乘上 $\frac{1-p_t}{1-u_t}$, 所以所邊必須要除$\frac{1-p_t}{1-u_t}$才會相等

$O(R|D,Q) = O(R|Q) \cdot \prod_{t:D_t=Q_t=1} \frac{p_t(1-u_t)}{u_t(1-p_t)} \cdot \prod_{t:Q_t=1} \frac{1-p_t}{1-u_t} \quad(7)$

右邊連乘積是 query not found in document
概念大概是將 query found in document 也計算進去,
不管有沒有出現在 document 都乘
整理後右邊連乘積的範圍就會和 document 無關
在對 document ranking 時就視為常數

$RSV_d = log \prod_{t:D_t=Q_t=1} \frac{p_t(1-u_t)}{u_t(1-p_t)} = \sum_{t:D_t=Q_t=1} log \frac{p_t(1-u_t)}{u_t(1-p_t)} \quad(8)$

取 log 後就得到 Retrieval Status Value(RSV),
log 是 monotonic function 不會改變 ranking 順序

RSJ Model:No Relevance Info

如果沒有給 relevance judgements,

• assume $p_t$ to be a constant
• Estimate $u_t$ by assume all documents to be non-relevant

1979 Croft&Harper

$\sum{t=1,D_t=Q_t=1}^{k} log \frac{N - n_t + 0.5}{n_t + 0.5}$

N: number of documents in collection
$n_t$ : number of documents in which term $D_t$ occurs

$\sum log( \frac{總文章數 - 某個字出現在文章次數 + 0.5}{某個字出現在文章次數 + 0.5})$

只看在 document 中和 query 相關的字,並加總每個字算出來的值

RSJ Model: with Relevance Info

• Maximum Lieklihood Estimate(MLE)
• Maximum A Posterior(MAP)

RSJ model 的 performance 還遠比不上 vector space model

Improving RSJ

• adding TF
• adding Doc.length
• query TF

改善後的最終公式稱作BM25

CH12 Language models for information retrieval

unigram language model

每個 word 只有單一的狀態,可以建立一個 table 放每個 word 對應到的機率

一個 string 出現的機率就是每個 word 的機率連乘積
Language model 應用：語音系統的語言校正

Language model 屬於 query generation process
每一篇 document 視為一個 language model
ranking 的計算是根據 P(Q|D)

計算 P(Q|D)

• Multinomial model
  

$P(q|M_d) = P((t_1,...,t_{|q|})|M_d) = \prod_{1 \leq k \leq |q|} P(t_k|M_d) = \prod_{distinct\;term\;t\;in\;q}P(t|M_d)^{tf_{t,q}}$

|q|: length of query
$t_k$ : query 的第 k 個位置的 token
$tf_{t,q}$ : term frequency of t in q

估計參數

• Maximun Likelihood Estimation(MLE)

  $\hat{P}(t|M_d) = \frac{tf_{t,d}}{|d|}$

hat符號表示估計值的意思

smooth the estimates to avoid zeros

避免 0 產生,相乘後結果很差

smooth 方法

1. Mixture model
   $P(t|d)=\lambda P(t|M_d) + (1-\lambda )P(t|M_c)$

   $M_c$ : the collection model
   $\lambda$ 的設定好壞會影響效能

   e.g.
   Collection = {$d_1,d_2$}
   $d_1$: Jack wants to play game
   $d_2$: Tom is cat
   query q: Tom game
   $\lambda = \frac{1}{2}$

   P(d|$d_1$) = [(0/5 + 1/8)/2]$\cdot$[(1/5 + 1/8)/2] $\approx$ 0.0101
   P(d|$d_2$) = [(1/3 + 1/8)/2]$\cdot$[(0/3 + 1/8)/2] $\approx$ 0.0143
   rank $d_2 > d_1$

Laplace smoothing

Text Generation with Unigram LM

• sampling
  由一個特定主題的 model,裡面會有各個字出現的機率(每一個 model 會有一個 distribution,機率分佈),取出一些機率較高的字可以形成 document
• estimation
  拿到一個 document,預估出 model

CH13 Text Classification and Naive Bayes

• Text Classification
• Naive Bayes
• Naive Bayes Theory
• Evaluation of Text Classification

Text Classification

standard supervised

1. Pre-define categories and lebel document
2. classify new documents

分類的方法

1. 人工判斷 準確但成本高
2. Rule-based 很多 if/else 的 rule,看到王建民就分類到體育新聞
   e.g. google Alert

3. Statistical/Probabilistic

   • Instance-based classifiers
     e.g. kNN
   • Discriminative classifiers
     學習出分隔的形式(一條線,一棵樹)
     資料少容易 overfit
     e.g. Decision tree,Neural Network
   • Generative classifier
     利用大量資料學習出分佈模型(mean,varience)
     e.g Naive Bayes

K-Nearest Neighbor Classifier(KNN)
Keep all train data
優點:不需要 training(每一個點都記錄下來)
缺點:不能做大量資料

Naive Bayes Classifier

arg max_c 找到一個 c(類別)使 P(c|d)最大 避免 under flow -> 取 log 連乘變成連加

機率會有零產生->避免這種情形全部機率做加 1

估計事前機率 是這個類別的機率和不是這個類別的機率 估計完這些係數 training 就結束

P(c|d) 給 document 判斷是哪個類別 P(c|d) = P(c)P(d|c)/P(d) 分母不考慮,和分類無關 且分子越大越好 P(d|c)可以拆成多個 Term 的連乘積 且假設每個字之間獨立

Feture Selection

• Reduces training time 挑特定的字訓練模型

Two idea

• Mutual information 計算字的交互作用,每一個字會有一個值,找 gap 最大的切開,拿比較相關的字做訓練
• CHI-Square statistic 用機率方法計算,算出機率高的就拿去做訓練資料

Evaluations 測試資料和 training data 不能有 overlapping

CH14 Vector Space Classification

• Rocchio classification
• kNN classification
• linear classification
• Bias-Variance Tradeoff

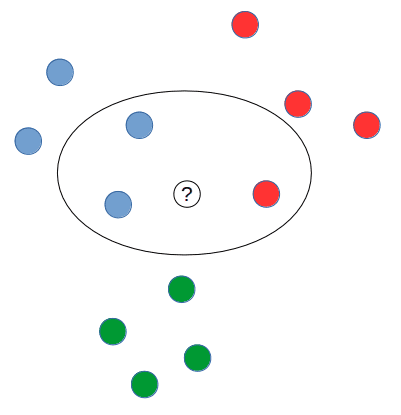
Vector Space Classification 基本假設

1. 資料如果同類會形成一個連續的空間
2. 資料如果不同類別,所形成的空間不會有 overlap

Rocchio classification(Nearest centroid classifier)

主要是沒有處理：

• nonconvex
• multimodal classes

應用：

• 1970 年 SMART 搜索系統中,應用在 relevance feedback

k Nearest Neighbors(kNN) classification

k = 1 過於 sensitive,太容易由某一類變成另外一類
k 太大結果過於模糊
k 通常選擇奇數(3,5,7),通常使用 heuristic 來決定 k 值

example: k = 3

計算相似度:

• Euclidean distance
• Hamming distance (binary instance)
• cosine similarity of tfidf

特色:

• 沒有任何學習
• 如果資料集很大,準確率非常高,資料集小可能就不會很準
• 大致上準確率會較 Naive Bayes 和 Rocchio 高
• Simple, expensive at test time, high variance, non-linear

Linear classification

$\sum{W_iX_i} > \theta, \quad \theta (threshold)$

線性分類器代表一個分界面,在一維代表一個點、二維代表一條線、三維代表一個平面

找到分界面的演算法分為兩類

1. Simple learning algorithms
   透過學習資料,學出分界面的參數

   • Naive Bayes,Rocchio,kNN

2. Iterative algorithms

   • Support vector machines,Perceptron

Linear Classifier 算是多個方法的集大成
e.g. Naive Bayes,Perceptron,Rocchio,Logistic regression,Support vector machines(with linear kernel),Linear regression with threshold

Bias-Variance Tradeoff

一種量測分類方法的指標

Bias-variance wiki

• Bias
  分類的結果和真實結果差距多少
  差距越大 Bisa 越高
• Variance
  比較每次猜出來的結果差異會不會很大

理想情形是 low Bias, low Variance

$Err(x) = Bias^2 + Variance + Irreducible Error$

Ch15 Support Vector Machines and Machine Learning on Documents

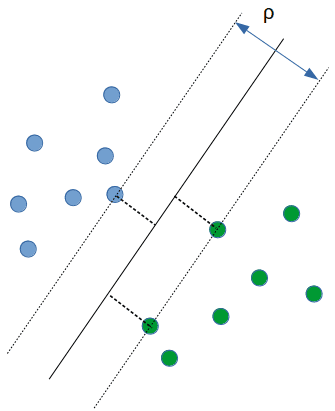
在 linear classification 中,分界線有無限多條,SVM 可以在這些線中找到一條最佳的線,而這條線只會由少數的點來形成。這些點是由分割上最困難的點所成的集合,集合稱作 support vector

要怎麼找到最佳的分割界面(hyperplane)
SVM 是從所有可能的分割界面中找到 geometric margin 最大的作為分割界面

Geometric Margin

訓練出來的線,兩端碰到最近的 support vector 中的點所為成的區域

目標是找到最大的$\rho$

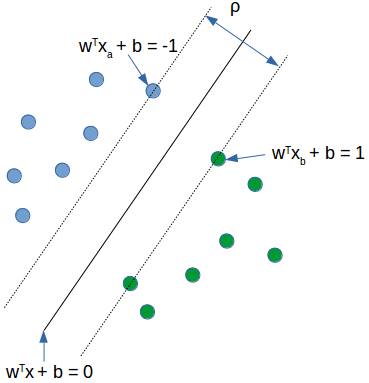
• w: hyperplane normal vector
• $x_i$: data point i
• $y_i$: class of data point (+1 or -1)
• classifier: f($x_i$) = sign($w^Tx_i$ + b) //b: bias
• Define functional margin of $x_i$ is $y_i(w^Tx_i+b)$

如果分到 1 類別帶入分類器會$\geq$1
分到-1 類別帶入分類器會$\leq$-1

$w^Tx_i + b \geq 1 \quad if\; y_i = 1$
$w^Tx_i + b \leq -1 \quad if\; y_i = -1$

$\rho = \frac{2}{\left \| w \right \|}$

quadratic optimization problem

找到 w 和 b 使$\rho = \frac{2}{\left \| w \right \|}$最大
$w^Tx_i + b \geq 1 \quad if\; y_i = 1$
$w^Tx_i + b \leq -1 \quad if\; y_i = -1$

較好的表示方法

要讓$\rho$最大,最小化$\left \| w \right \|$
找到 w 和 b 使$\phi(w) = \frac{1}{2} \left \| w \right \|$最小
$y_i(w^Tx_i + b) \geq 1$

希望$y_i和(w^Tx_i$ + b)同號
也就是希望分類結果和帶入分類器結果是同號

dual problem

每一個線性規劃的問題(primary problem)都有一個對映的線性規劃問題(dual problem),解決 dual problem 就可以得到原來問題的解

解決上面問題的 dual problem
Lagrange multiplier

找到$\alpha_1,...,\alpha_N$使$\sum{\alpha_i-\frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_j\vec{x}_i^T\vec{x}_j}$最大

• $\sum{\alpha_iy_i} = 0$
• $\alpha_i \geq 0 \quad for \; all \; 1 \leq i \leq N$

solution

$\vec{w}=\sum\alpha_iy_i\vec{x}_i$
$b = y_k-\vec{w}^T\vec{x}_k\quad for\; any\; \vec{x}_k \; such\; that\; \alpha_k \neq 0$

大多數的點$\alpha_i = 0$代表不重要的點,而非零的$\alpha$代表為 support vector

分類的 function

$f(\vec{x}) = sign(\sum\alpha_iy_i\vec{x_i}^T\vec{x} + b)$

soft margin classification 允許某些點可以分錯 $\phi$(w) 1/2||w|| + C$\sum$ slack C 越小越可以容錯 因為希望$\phi$(w) 出來的值可以越小越好

Non-linear SVMs

用一條線分不開的情形, svm 提供 kernel function 的概念,將點 map 到更高維的空間中,就有機會能夠分割

kernel function $K(x_i,x_j)=x_i^Tx_j$

透過 kernel function 可以知道高維空間的內積值

Common kernels

• Linear
• Polynomial
• Radial basis function(infinite dimensional space)

Ch16 Flat clustering

Classification 分類 vs. Clustering 分群

• supervised learning
• Unsupervised learning 資料沒有 label,沒有正確答案
• reinforcement learning

Flat vs. Hierarchical clustering

• Flat

  • Hard clustering 一個東西就只能分到一類
    e.g. K-means
  • Soft clustering
    比較偏向使用機率分群
• Hiearchical clustering
  希望分群完後是一種階層架構

K-means

• Each cluster in K-means is defined by a centroid

Method

• reassignment of vector
• recomputation of centroids
• init 隨機給重心點
• reassign
• recomputation of centroids

什麼時候收斂？ RSS(residual sum of squares) 每次的 centroid 差值小於某個值就停止

缺點是 initial 的點很糟結果會不好和 k 怎麼決定

time complexity O(IKNM)

Evaluation

• Internal criteria RSS 的評估

• External criteria goal base,必須要知道正確答案

  • Purity 必須要有正確答案,並和分出的結果做比較

怎麼決定 k 值

1. 外部資訊
2. 從 1 開始慢慢加上去,並且計算 criteria 是否有增加

Ch21 Link Analysis

• Anchor Text
• Citation Analysis
• PageRank
• HITS: Hub & Authorties

Citation Analysis

Citation frequency can be used to meature impact

PageRank

model behind Random walk 在所有網頁上隨機走動,且根據 link 連到其他網頁 到穩定狀態(steady state)後,計算停留在每個 page 的機率 PageRank = long-term visit rate

將網頁連結的關係使用矩陣來存 Dead end,如果有一些網頁指到同一個網頁如果之後就跳不出去會有 not well define 的問題 teleporting 解決這個問題,給一個很低的機率讓所有 0 的網頁都有機會跳到別的網頁, 類似 smoothing, 每個點會有一個機率,且乘上矩陣一次會走一步 那一直走下去會到收斂狀態($\pi$)

P is transifer matrix $\pi = \pi P$

Power method -> 一直乘 P,直到向量收斂

HITS & Authorities

1. Hub 像是入口網站,有很多連出去的連結(out link)
2. Authorities 網站內的資料是屬於比較官方的網站 資料屬於比較權威(就是多的 link 指向的網頁)

不停的迭代 $h = Aa$
$a = A^Th$

A 代表相鄰矩陣 a 的初始值($a_0$)在第一輪都設定為一樣